September 2 to 5, 2025
Invited speakers:
- Francesco Lin (Columbia), The interplay between gauge theory and the geometry and topology of hyperbolic 4-manifolds
- Bruno Martelli (Pisa), The algebraic topology of higher dimensional hyperbolic manifolds, generalizations of the virtual fibering conjecture to higher dimensional manifolds and connections with geometric group theory
- Ben Lowe (Chicago), Characterizing arithmeticity in dimensions > 2 using totally geodesic submanifolds
- Chris Leininger (Rice), Surface bundles and coarse geometry
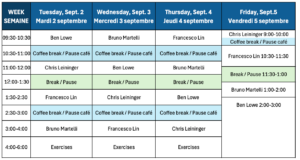
Schedule:
Abstracts:
- Francesco Lin (Columbia), The interplay between gauge theory and the geometry and topology of hyperbolic 4-manifolds
TBA
- Bruno Martelli (Pisa), The algebraic topology of higher dimensional hyperbolic manifolds, generalizations of the virtual fibering conjecture to higher dimensional manifolds and connections with geometric group theory
It is an interesting open question to understand to which extent Thurston’s revolutionary work on hyperbolic manifolds may extend from dimension 3 to higher. We will show during this minicourse that this higher-dimensional extension holds at least in some cases. We will start by introducing hyperbolic Coxeter polytopes, and various techniques to build higher dimensional hyperbolic manifolds. Then we will investigate their topology, and concentrate on those that are known to fiber over the circle – or at least to admit some interesting circle valued map.
- Ben Lowe (Chicago), Superrigidity and Differential Geometry
Discrete subgroups of semisimple Lie groups, or equivalently nonpositively curved locally symmetric spaces, are central objects in most areas of modern mathematics. The first part of the minicourse will treat the Mostow-Margulis (super-)rigidity theorems, which give a structural understanding of nonpositively curved finite volume locally symmetric spaces and the possible maps between them. A great achievement of this theory is Margulis’s arithmeticity theorem, which states that finite volume higher rank locally symmetric spaces (e.g., corresponding to discrete subgroups of SL(n,R) for n>2) must be arithmetic, or must correspond to discrete subgroups obtained by a procedure analogous to taking the integer points of a group of matrices. Although this statement fails in rank one, recently Bader-Fisher-Miller-Stover and Margulis-Mohamaddi proved an analogue of the Margulis arithmeticity theorem in the rank one setting of finite volume real hyperbolic manifolds: namely, if such a manifold contains infinitely many maximal finite volume totally geodesic submanifolds of dimension greater than one, then it must be arithmetic. I will give a gentle overview of this area taking care to explain necessary background and definitions.
In the second part of the minicourse, I will describe a research program that attempts to prove analogues of the above results in the broader setting of differential geometry. Work in this direction has drawn on several different parts of mathematics, including dynamical systems, representation theory, and geometric analysis. After surveying some of the foundational results including work by Mok-Siu-Yeung and Besson-Courtois-Gallot, I will describe recent work of myself and work joint with Filip-Fisher that proves versions of the Bader-Fisher-Miller-Stover and Margulis-Mohamaddi arithmeticity theorem for finite volume negatively curved manifolds. I will also describe some of the many open problems and directions for future research in this area.
- Chris Leininger (Rice), Surface bundles and coarse geometry
Thurston’s Hyperbolization Theorem for Haken 3-manifolds required special treatment of those 3-manifolds that are surface bundles over the circle. A major part of his proof involved translating the atoroidal condition for the 3-manifold into a dynamic/geometric condition for the monodromy homeomorphism: this is the content of Thurston’s celebrated Classification Theorem for the mapping class group, and relied on an analogy with isometries of hyperbolic space (and particularly its compactification). For surface bundles over spaces that are more complicated than the circle, a coarse hyperbolization program was instigated at the end of the last century by Farb and Mosher, again drawing on analogies with Kleinian groups acting on hyperbolic space. This program has been developed considerably by Kent-Leininger, Hamenstädt, Mj-Sardar, Durham-Taylor, and many others. Two of the driving questions in this area are: (1) Are atoroidal surface bundles Gromov hyperbolic? (2) Are there Gromov hyperbolic surface bundles over surfaces? There has been incremental progress on question (1) over the years with affirmative answers given under a variety of additional hypotheses, but very little progress on problem (2) until last year.
In the first lecture, I will begin with a review of Thurston’s theorems, providing motivation for the general theory, then describe some generalities for surface bundles and their monodromy, as well as introducing some important objects in the topic, including mapping class groups, Teichmüller spaces, and the curve complex. In the second lecture, I’ll describe Farb and Mosher’s notion of convex cocompactness and it’s connection to Gromov hyperbolicity of surface bundles, its numerous equivalent formulations and relationship to Kleinian groups, and partial answers to question (1). In the third lecture, I’ll describe my recent work with Kent constructing the first examples of atoroidal surface bundles over surfaces, and indicate why these *should* ultimately lead to a positive answer to question (2). In the last lecture, I will discuss generalizations of convex cocompactness to geometric finiteness in the mapping class groups, work with Dowdall, Durham, and Sisto where we have begun extending hyperbolicity features of the bundles to this setting, and a variety of open questions related to this new direction of research.






