Le modèle à 2 compartiments

Dans ce type de modèle, en plus du compartiment \[C_1(t)\] qui représente la concentration de médicament dans le sang, il y a un deuxième compartiment, \[C_2(t)\], qui représente la concentration de médicament dans les tissus ou les organes. L’inclusion de ce deuxième compartiment est nécessaire dans certains cas puisqu’il affecte drastiquement la forme de la décroissance de la concentration du compartiment \[C_1(t)\]. L’observation de deux pentes dans la phase terminale de la courbe de la concentration appuie la validité d’un modèle à 2 compartiments pour représenter correctement les phases de distribution et d’élimination.

\[\frac{dC_1(t)}{dt} = -k_{élim}C_1(t)\,-\,k_{12}C_1(t) + k_{21}C_2(t)\]

\[\frac{dC_2(t)}{dt} = k_{12}C_1(t)\,-\,k_{21}C_2(t)\]

Cliquez sur les pastilles ci-dessous pour visualiser le fonctionnement du modèle à 2 compartiments.

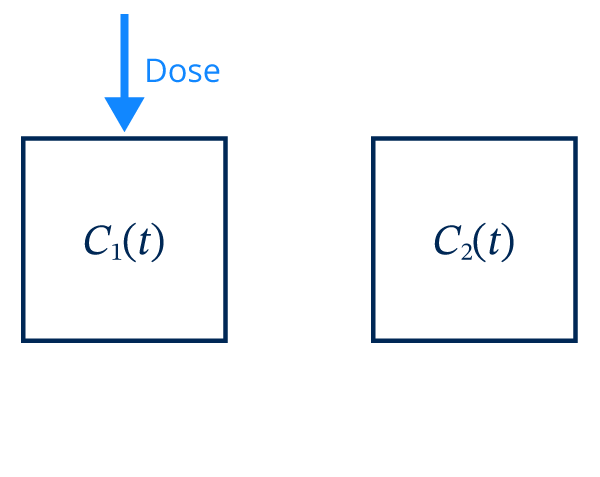Il y a libération du médicament dans l’organisme.

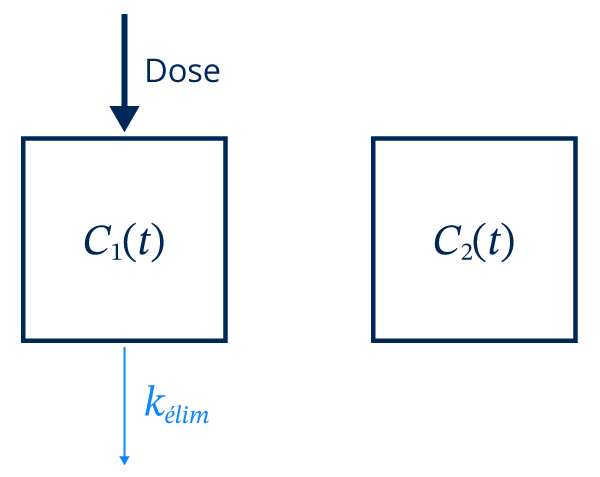On observe alors une décroissance rapide de la concentration du compartiment central puisque le médicament est éliminé par l’organisme à un taux \[k_{élim}\].

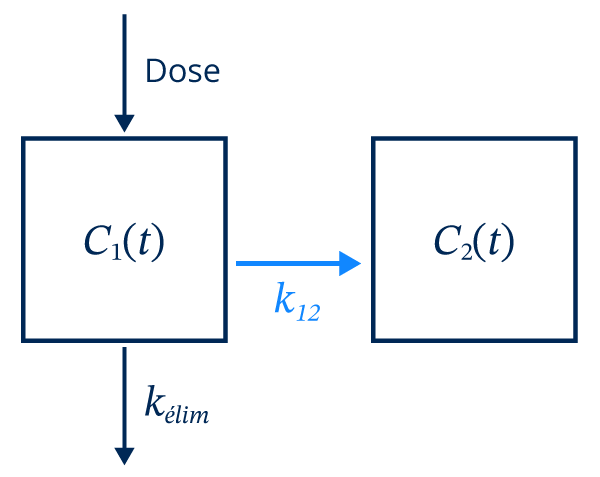Le médicament est également transféré aux tissus du site d’action à un taux \[k_{12}\].

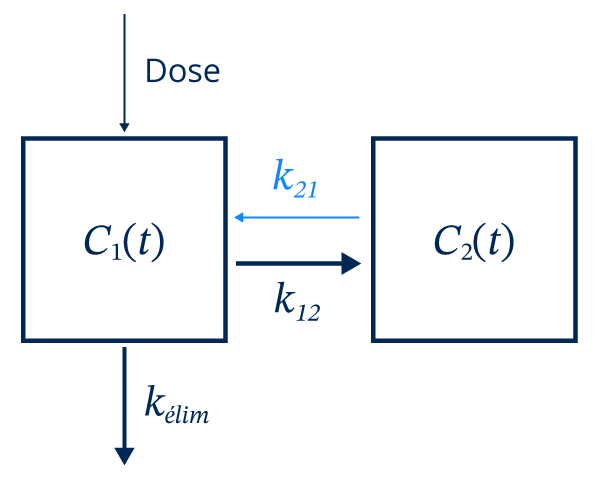Puisqu’il y a aussi un transfert du médicament des tissus vers le sang, il y a un autre taux, le paramètre \[k_{21}\], qui est présent dans le modèle.

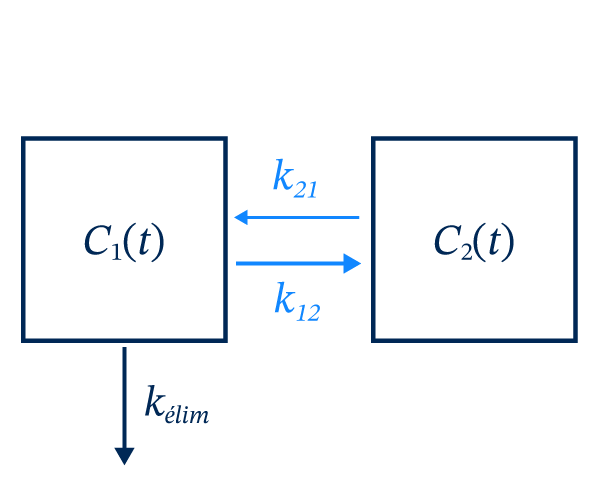L’échange entre les compartiments se déroule jusqu’à l’atteinte d’un équilibre.

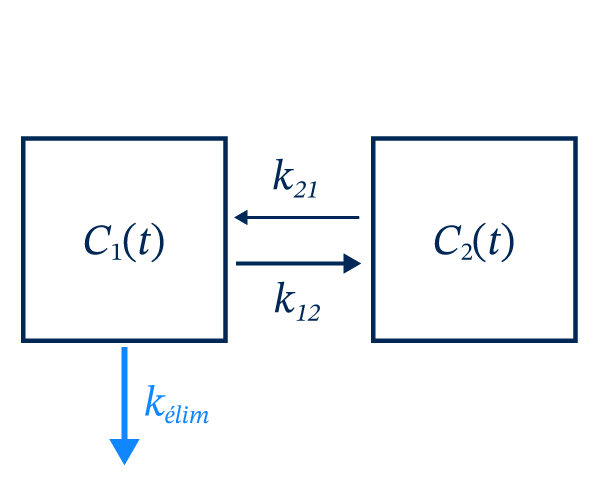Par la suite, seule l’élimination est responsable de la décroissance de la concentration du compartiment central, ce qui mène à la deuxième phase de décroissance qu’on peut observer dans un graphique semi-log.

Dans le graphique suivant, il est possible de faire varier les trois paramètres \[k_{élim}\], \[k_{12}\] et \[k_{21}\] de l’équation pour en voir les effets sur les courbes.

Dépendamment de la forme des données de concentration dans un graphique semi-log, le nombre de compartiments du modèle doit être établi avant de paramétrer le modèle. S’il n’y a qu’une droite, un modèle à 1 compartiment est suffisant ; mais si on observe 2 phases, alors un modèle à 2 compartiments est plus approprié.