Le modèle à 1 compartiment

Dans ce type de modèle, il n’y a qu’un seul compartiment : il représente la concentration de médicament dans le sang qui va suivre une courbe exponentielle décroissante. Comme vu dans la section « Quelques notions de base », l’équation différentielle linéaire représentant la concentration \[C_1(t)\] dans le compartiment s’écrit ainsi :

\[\frac{dC_1(t)}{dt}=- k_{élim} ⋅ C_1(t)\]

La décroissance exponentielle s’analyse plus facilement en utilisant une échelle logarithmique sur l’axe vertical (c’est-à-dire un graphique présenté en semi-log). De cette façon, on observe une droite décroissante dont la pente représente le paramètre d’élimination \[k_{élim}\].

Voici une représentation du modèle à 1 compartiment.

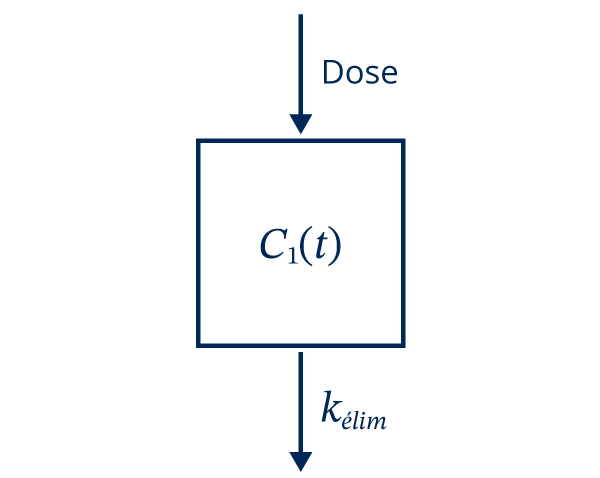
Dans le graphique suivant, il est possible de faire varier le paramètre \[k_{élim}\] de l’équation pour en voir les effets sur les courbes.