Le diagramme de flux

Une autre raison de privilégier une fonction sous la forme d’une équation différentielle est qu’il est plus facile d’y représenter les différentes interactions qui peuvent affecter la population dans le temps. Si on décortique la variation d’une population cellulaire, on observe des naissances et des morts qui se représentent très facilement à l’aide d’un diagramme de flux.

Cliquez sur les pastilles ci-dessous. Cette animation montre un exemple de diagramme composé d’un compartiment qui représente la population, et de flèches d’entrées et de sorties qui représentent les variations positives et négatives qui affectent cette population. Quant aux paramètres \[β\] et \[δ\], ils servent à représenter respectivement les taux de naissance et de mort qui sont proportionnels à la population.

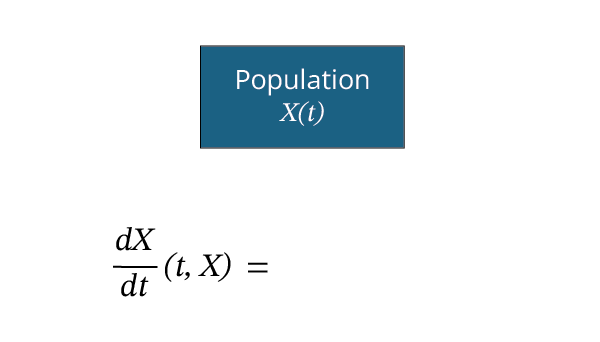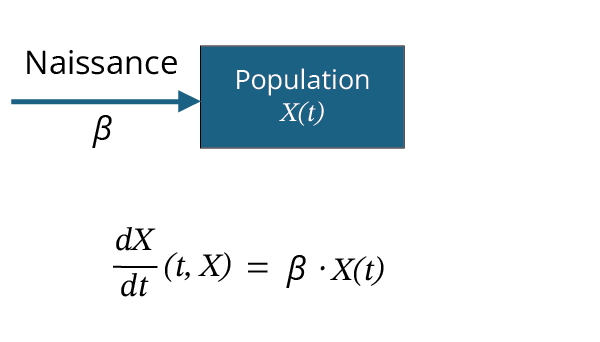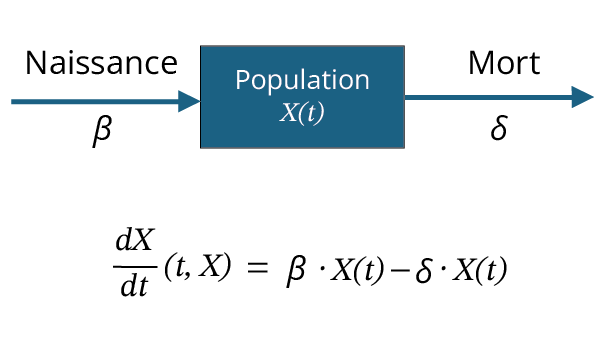On peut donc transformer ce diagramme de flux sous la forme d’une équation différentielle pour la population \[X(t)\]. On observe alors un terme d’entrée (positif) linéaire et un terme de sortie (négatif) linéaire. Néanmoins, cette notation reste équivalente à la forme présentée auparavant avec le paramètre \[λ\].

\[\frac{dX}{dt}=β⋅X-δ⋅X=(β-δ)⋅X=λ⋅X\]

Dans cette équation :

• si \[β>δ\], cela implique que le taux de naissance est supérieur au taux de mortalité, alors \[λ\] sera plus grand que zéro \[(λ > 0)\] et la dérivée sera positive : la fonction va croître.
• si \[β<δ\], cela implique que le taux de naissance est inférieur au taux de mortalité, alors \[λ\] sera plus petit que zéro \[(λ<0)\] et la dérivée sera négative : la fonction va décroître.

Dans ce cas, on peut alors considérer \[λ\] comme étant la croissance « effective », c’est-à-dire la différence entre le taux de naissance et le taux de mortalité de la population de cellules tumorales.